
Prime numbers are defined to be a class of counting numbers (1, 2, 3, 4, 5. But there's nothing to stop us inventing similar words for 5, 7, 11 or any of the other primes. For some reason, though, we have no such a word. would all be "treven numbers" and 3 would be the only "treven prime". If we invented the word treven to mean "can be divided into 3 equal whole number amounts", then 3, 6, 9, 12, 15. 2 is even, but it's only divisible into two equal "piles of one" and you'll remember that this doesn't count, so 2 is prime. ) can be divided by 2 – that's what makes them even! And because they're divisible by 2 – you can divide them into two equal piles – they can't be prime numbers. All even numbers larger than 2 (that is, 4, 6, 8, 10, 12. We just happen to have a word in our language ("even") which, when applied to a counting number, means can be divided into two equal whole number amounts. People sometimes dwell on this fact, but there's really nothing remarkable about it. This is why finding new, ever-larger primes requires such huge computational resources. Regardless of any shortcuts, though, as counting numbers get larger, checking them for "primeness" tends to take longer. And in the case of 29, we'd only need to check divisibility of numbers up to 5 (the largest counting number less than the square root of 29). In practice, there are many shortcuts: for example, if a number bigger than 2 is even then it isn't prime, and if a number bigger than 5 ends with the digit 0 or 5 then it isn't prime. The most straightforward way is to check all smaller counting numbers (after 1) to see if it divides by them.

Equivalently, a prime is a counting number which cannot be obtained by multiplying two smaller counting numbers. One way of avoiding problems with 1 in the definition of prime numbers is to define a prime to be any counting number that is divisible by exactly two counting numbers (which will be 1 and the number itself), because 1 is then excluded, only being divisible by one number (itself). I've even seen one argument invoking the Old Testament to "prove" that 1 is a prime! But, ultimately, like arguing about whether or not something is "art", it comes down to the definition of a word.
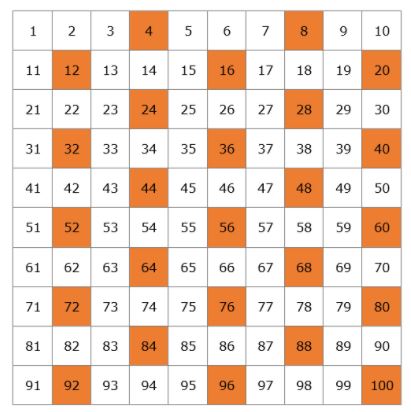
#LIST OF PRIME NUMBERS BETWEEN 1 AND 100 PROFESSIONAL#
These tend to be mathematical enthusiasts presenting elaborate arguments on webpages rather than professional mathematicians contributing to the academic literature. Despite this, some people still feel driven to dispute the assertion that "1 is not a prime number". Having hugely expanded their understanding of the number system, many good reasons emerged why we should not consider 1 to be in the same category as 2, 3, 5, 7, 11, 13, . It turns out that 1 is now considered not to be a prime number, but up until the late 1800s it generally was. On the other hand, one stone can't be arranged in a "rectangular grid" as I described above. After all, 1 is only divisible by 1 and itself (which are the same thing!). So 8, 9 and 10 are not prime, but 11 is.įrom the definition/explanation above, you wouldn't be able to tell. Eight stones can be arranged in a 2×4 grid, nine stones in a 3×3 grid, ten stones in a 2×5 grid, but eleven stones cannot be arranged in a rectangular grid (a 1×11 grid doesn't count as "rectangular", otherwise this explanation would be pointless). A more intuitive way of grasping what a prime number is involves trying to arrange a number of stones (or beans, or whatever) into a rectangular grid. That's the definition usually taught in schools. A prime number is a counting number which can't be divided, except by 1 or itself (every counting number can be divided by 1 and itself).


What do we know about the gaps between consecutive primes numbers?.Do you get different prime numbers if you switch from base-10 to another base for representing numbers?.Why do people search for large prime numbers?.How are prime numbers used in cryptography?.Is it true that prime numbers have been used in attempts to communicate with extra-terrestrials?.Do prime numbers show up in the natural world?.Is there a pattern in the prime numbers?.Is there a formula for finding prime numbers?.2 is the only even prime number – why is that?.How can you tell if a number is prime or not?.Frequently asked questions about prime numbers:


 0 kommentar(er)
0 kommentar(er)
